Matrizes

Matrizes são organizações de informações numéricas em uma tabela retangular formada por linhas e colunas. Essa organização em uma tabela facilita que se possa efetuar vários cálculos simultâneos com as informações contidas na matriz.

Definição de matrizes
Toda matriz tem o formato m x n (leia-se: m por n, com n e m ∈ N*), onde m é o número de linhas e n o número de colunas.

Representação de matrizes
Existem diversas maneiras de representarmos matrizes, veja quais são:

Colchetes: [ ]
Parênteses: ( )
Barras Simples: | |
Barras Duplas: || ||
Essas são as representações mais comuns que encontramos na literatura.

Exemplos:



Elementos de uma matriz

Seja a matriz genérica Amxn, isto é, m representa as linas e n o número de colunas. Então, temos:

Elementos de uma matriz
Seja a matriz genérica Amxn, isto é, m representa as linas e n o número de colunas. Então, temos:



Dessa forma, os elementos da matriz A são indicados por aij, onde o i representa o índice da linha e j representa o índice da coluna para o elemento em questão. Assim, para localizar um elemento na coluna, procura-se o número da linha e da coluna, esses números são os índices i e j.

Pela imagem acima, veja que as linhas são numeradas da esquerda para a direita, enquanto que as colunas são numeradas de cima para baixo.

Matriz Quadrada

É uma matriz em que o número de colunas é igual ao número de linhas. Sendo que uma matriz quadrada de ordem mxn podemos dizer que ela tem ordem n

Exemplo:

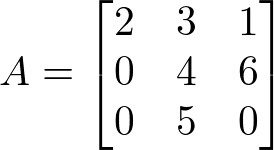
Matriz Diagonal

É uma matriz quadrada em que todos os elementos que não pertencem a diagonal principal são nulos.

Exemplo:

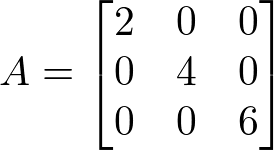
Matriz Identidade

É uma matriz quadrada em que todos os elementos que não pertencem a diagonal principal são nulos e os elementos da diagonal principal são 1. É representada por In, matriz quadrada de ordem n.

Exemplos

I2 = Matriz identidade de ondem 2

I3 = Matriz identidade de ondem 3

Matriz Transposta

Uma matriz transposta é uma matriz resultante da troca ordenadamente de linhas pelas colunas de outra matriz. Se temos uma matriz A, então a transposta de A tem notação At.

Exemplo:

Seja a matriz A = [aij]mxn a matriz transposta de A é At = [aij]nxm.



Multiplicação entre Matrizes

Considere as matrizes Amxn e Bnxp. A multiplicação das matrizes A e B, nesta ordem, resulta em Cmxp, de forma que C seja obtida pela soma dos produtos dos elementos da linha i de A e da coluna j de B.

Exemplo:

Considere as matrizes A e B, então A x B é:



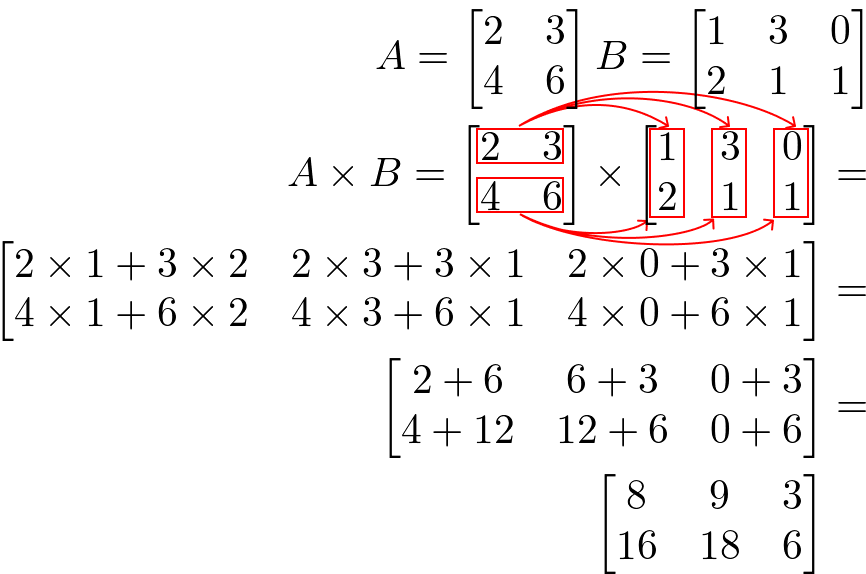
Observações importantes:

A multiplicação de matriz somente é possível se o número de linhas em uma matriz for igual ao número de colunas da outra matriz.
A matriz resultante C tem o mesmo número de linha da primeira matriz e o mesmo número de colunas da segunda matriz.